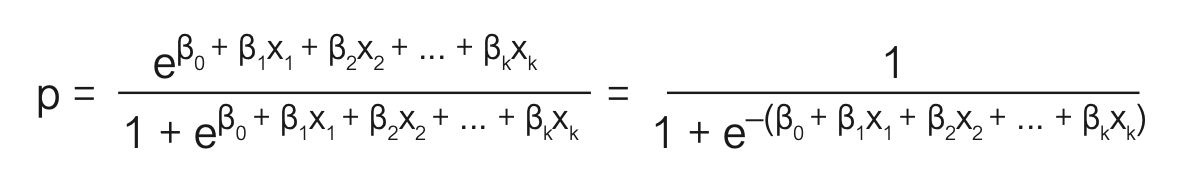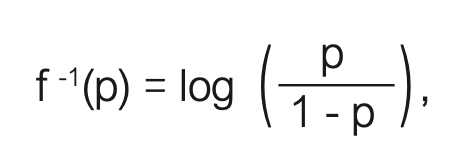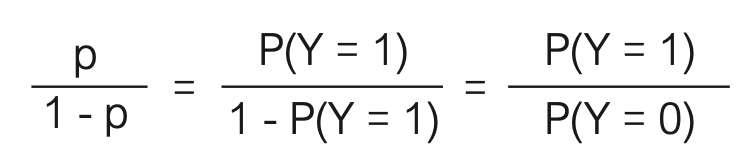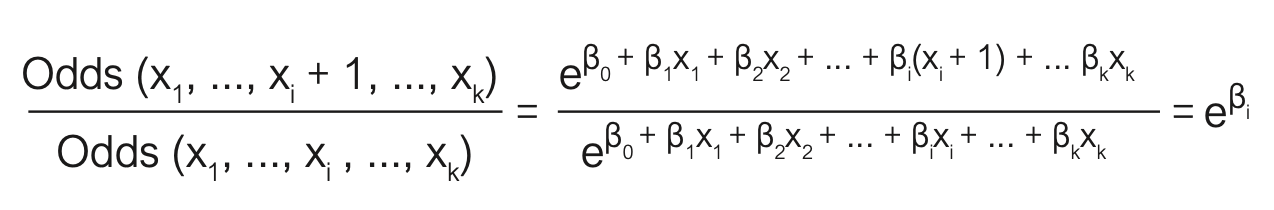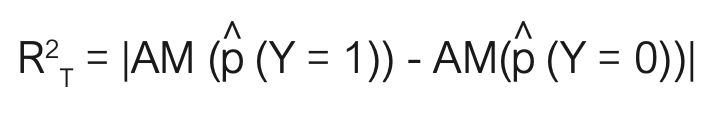Fazitbox

Pro und Contra logistische Regression:

Pro

• Analog zum linearen Modell lassen sich ANOVA- und ANCOVA-Modelle definieren, wobei man anstelle der Varianz die Devianz betrachtet.
• Anstelle des Bestimmtheitsmaßes R2 können im Fall der logistischen Regression verschiedene Pseudo-R2 zur Untersuchung der Modellanpassung verwendet werden. Alternativ hierzu sind auch AIC und BIC möglich.
• Die logistische Regression kann auch für die binäre Klassifikation Anwendung finden.

Contra

• Ein logistisches Modell sollte immer einer gründlichen Modelldiagnostik unterzogen werden.
• Das Simpson Paradoxon und Multikollinearität sind auch bei der logistischen Regression zu beachten und sollten bei der Interpretation und Diskussion der Ergebnisse einbezogen werden.
• Wird eine statistische Modellwahl durchgeführt, so sollte dies mit großer Sorgfalt und unter Verwendung einer internen oder externen Validierung erfolgen.

Einführung

In der Medizin und Epidemiologie spielen binäre/dichotome Response-Variablen eine sehr wichtige Rolle. Sie dienen zum Beispiel dazu, um Mortalität, Letalität, Inzidenz oder Prävalenz zu untersuchen. Falls die Response von gewissen erklärenden Variablen abhängt, führt uns dies auf die logistische Regressionsanalyse. Wir haben diese bereits kurz in einem vorangegangenen Tutorial angesprochen [1]. Darüber hinaus wird die logistische Regression auch häufig für die binäre Klassifikation verwendet. Wir werden in diesem Tutorial kurz das multiple logistische Modell vorstellen und auf wichtige Aspekte eingehen, die in der Praxis zu beachten sind. Zur Demonstration führen wir außerdem anhand eines Praxisbeispiels eine logistische Regressionsanalyse durch.

Multiple logistische Regression

Wie in [1] besprochen, führt uns die Betrachtung eines binären Merkmals Y auf die Bernoulli- oder Binomial-Verteilung, wobei die Erfolgswahrscheinlichkeit P(Y = 1) = p  [0, 1] unbekannt ist. Wollen wir den Einfluss von k ³ 1 unabhängigen Variablen auf p untersuchen, so können wir hierfür nicht den direkten Modellansatz

verwenden, da die rechte Seite der Gleichung unbeschränkt ist. Wenn wir hierauf aber die Transformation

anwenden, welche die reellen Zahlen auf das Intervall (0, 1) abbildet, ändert sich die Situation. Wir erhalten

Die Funktion f entspricht einer logistischen Funktion und er- gibt sich auch als Verteilungsfunktion der logistischen Verteilung. Manchmal wird diese auch als expit-Transformation bezeichnet in Analogie zu ihrer Umkehrfunktion

welche üblicherweise logit-Transformation genannt wird. Nutzen wir diesen Zusammenhang, so ergibt sich

das multiple logistische Regressionsmodell (vgl. Abschnitt 8.4 in [2]). Der Ausdruck

wird auch Chance oder Odds genannt. Bei der logistischen Regression handelt es sich demnach um ein lineares Modell für die log-Odds. Die logistische Regression ist außerdem ein spezielles generalisiert lineares Modell, wobei man in diesem Zusammenhang die logit-Transformation auch als Linkfunktion bezeichnet. Die Parameter β0, β1, …, βk können dabei mit Hilfe der Maximum-Likelihood-Methode geschätzt werden, wobei hierfür ein iteratives Verfahren zum Einsatz kommt, das sogenannten Fisher-Scoring. Die Interpretation der Koeffizienten ist im Fall der logistischen Regression etwas schwieriger und man wendet hierfür üblicherweise die e-Funktion auf das Modell an (vgl. Abschnitt 8.4.3 in [2]). Dies führt uns auf

Ändern wir den Wert einer unabhängigen Variable xi um eine Einheit und lassen die anderen unabhängigen Variablen unverändert, so erhalten wir

Die Größe eβi beschreibt demnach das Chancenverhältnis (Odds-Ratio) bei der Veränderung der Variable xi um eine Einheit. Da die anderen k–1 unabhängigen Variablen im Modell unverändert bleiben, spricht man auch von einer adjustierten Odds-Ratio, adjustiert auf die anderen k–1 unabhängigen Variablen. Der Koeffizient eβi wird auch als Einfluss- oder Effekt-Koeffizient bezeichnet. Erhält man einen Wert <1, so hat die Veränderung einen negativen Einfluss/Effekt auf die Odds-Ratio. Ein positiver Einfluss/ Effekt auf die Odds-Ratio liegt vor, falls eβi > 1 ist.

Das logistische Modell basiert auf weniger Voraussetzungen als das lineare Modell (vgl. [3]). Im Wesentlichen muss es einen inhaltlich begründeten (linearen) Zusammenhang zwischen den Regressoren und der log-Odds geben, wobei die Beobachtungen voneinander (stochastisch) unabhängig sein müssen (keine Zeitreihe).

In der logistischen Regression tritt an die Stelle der Residuenquadrate RSS (residual sum of squares) der linearen Regression (vgl. [3]) die sogenannte Devianz (vgl. Abschnitt 8.4.1 in [2]). Folglich spricht man dann auch von einer Devianzanalyse (analysis of deviance) anstatt von einer Varianzanalyse (analysis of variance). Die Nullhypothese H0 : βi = 0 kann (asymptotisch) mit Hilfe eines z-Tests unter- sucht werden. Alternativ kann hierfür auch ein sogenannter Likelihood-Verhältnistest (ein χ2-Test), der auf der Devianz basiert, herangezogen werden.

Es können für logistische Modelle analog zum linearen Modell auch ANOVA- und ANCOVA-Modelle definiert werden, wobei anstelle der Varianz die Devianz analysiert wird.

Für die Modelldiagnostik verwendet man nicht die Residuen wie bei der linearen Regression [3], sondern die sogenannten Devianz- und Pearson-Residuen. Wir verzichten hier auf die Definition dieser Residuen und verweisen statt- dessen auf Abschnitt 8.4.5 in [2]. Falls das Modell korrekt ist, sollten diese Residuen zumindest näherungsweise einer Normalverteilung folgen (vgl. Abschnitt 8.4.5 in [2]).

Da das Bestimmtheitsmaß R² auf der Varianz basiert, kann es im Fall der logistischen Regression nicht zur Beurteilung der Güte der Anpassung herangezogen werden. Stattdessen kommen hierfür sogenannte Pseudo-Bestimmtheitsmaße R² zum Einsatz, welche sich aus der Devianzanalyse ergeben (vgl. Abschnitt 8.4.6 in [2]). Man vergleicht die Likelihoods (L) oder log-Likelihoods (logL) von Modell und Nullmodell (Modell mit 0 Regressoren). Bekannte Pseudo- Bestimmtheitsmaße sind:

Eine weitere Alternative ist das Pseudo-R² von Tjur [7], welches ursprünglich von Tjur als Diskriminationskoeffizient (coefficient of discrimination) bezeichnet wurde:

Es wird in diesem Fall das arithmetische Mittel (AM) der vor- hergesagten Wahrscheinlichkeiten für Beobachtungen mit Y = 1 mit dem AM der vorhergesagten Wahrscheinlichkeiten für Beobachtungen mit Y = 0 verglichen. Neben diesen Pseudo-R²-Werten können auch das Akaike und das Bayessche Informationskriterium (AIC und BIC) für den Vergleich von Modellen herangezogen werden [3].

Das Simpson-Paradoxon und Multikollinearität können auch im Rahmen einer logistischen Regressionsanalyse auftreten (vgl. [3]). Für die Modellwahl gibt es im Fall der logistischen Regression analoge Ansätze wie im Fall der linearen Regression, die mit ähnlichen Einschränkungen verbunden sind (vgl. [3]).

Da das logistische Regressionsmodell auch für die binäre Klassifikation verwendet werden kann, können zur Beurteilung der Ergebnisse auch die entsprechenden Methoden der binären Klassifikation wie etwa die Analyse der ROC (receiver operating characteristic)-Kurve herangezogen werden [8]. Dies geht jedoch über die Zielsetzung dieses Tutorials hinaus.

Beispiel

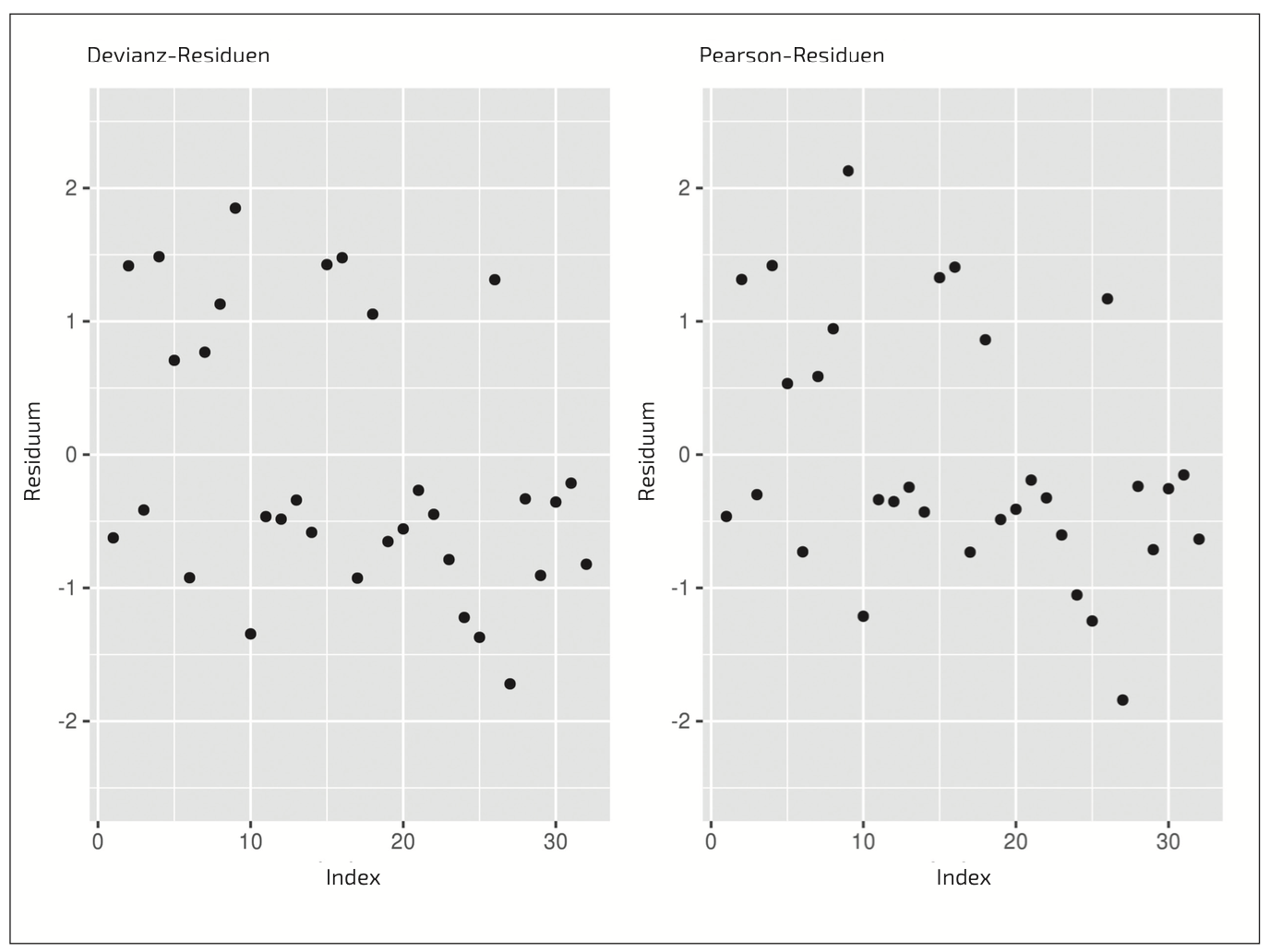
Wir greifen das Beispiel zur 30-Tage-Mortalität aus dem Tutorial 10 auf [1]. Wir betrachten nur Kinder mit hypoplastischem Linksherzsyndrom, die einer Herzoperation mit extrakorporaler Zirkulation unterzogen wurden. Des Weiteren betrachten wir nur die beiden Kardioplegieverfahren Custodiol (CCC) und pädiatrische Mikroplegie (MBC). Aus einem großen Datensatz mit 1061 Kindern erfüllen 45 Kinder diese Kriterien, wobei 10 der Kinder innerhalb von 30 Tagen nach der Operation (OP) verstarben. Da alle verstorbenen Kinder sehr jung waren (max. 12 Tage), schränken wir den Datensatz weiter ein und schließen nur Kinder ein, die bei der OP maximal 14 Tage alt waren. Dies reduziert den Datensatz auf 32 Kinder. Wir untersuchen mit Hilfe einer logistischen Regressionsanalyse den Einfluss des Kardioplegieverfahrens auf die 30-Tage-Mortalität, wobei wir auf die Ischämiezeit (in Minuten), den VIS-Score und das Gewicht (in Kilogramm) ad- justieren. Bei 8 Kindern wurde CCC eingesetzt, wobei hiervon zwei verstorben sind. Im Fall von MBC sind 8 der 24 Kinder verstorben. Die Residuen in Abbildung 1 wirken zufällig und zeigen keine auffälligen Strukturen.

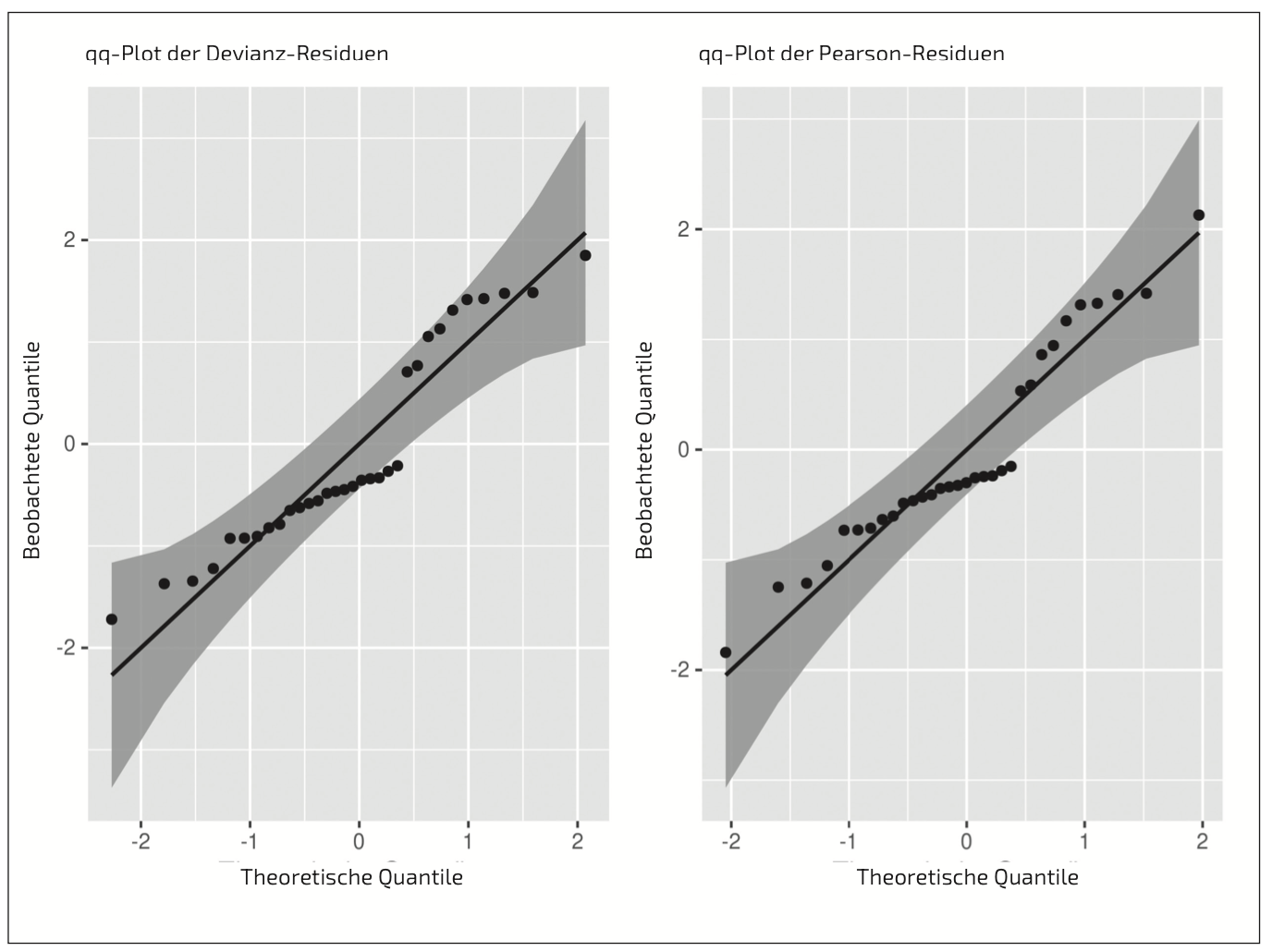
Die qq-Plots der Residuen in Abbildung 2 bestätigen, dass wir zumindest näherungsweise von einer Normalverteilung der Residuen ausgehen können.

Für die Pseudo-R²-Maße erhalten wir durchweg recht ähnliche Werte: R_2F = 0,20, R²_CS = 0,22, R²_N = 0,31 und R²_T = 0,22. Die Werte deuten auf ein akzeptables Modell hin (vgl. Abschnitt 8.4.6 in [2]).

Sowohl einzeln betrachtet als auch im multiplen Regressionsmodell ergibt sich für das Kardioplegieverfahren (z-Test: p = 0,506, χ2-Test: p = 0,494) kein signifikanter Effekt auf die 30-Tage-Mortalität. Auch die Ischämiezeit (z-Test: p = 0,355, χ2-Test: p = 0,345, adj. OR (CI95): 2,19 (0,22 – 22,0)) und der VIS-Score (z-Test: p = 0,675, χ2-Test: p = 0,672, adj. OR (CI95): 0,99 (0,96–1,01)) haben keinen signifikanten Effekt auf die 30-Tage-Mortalität. Im Fall des Gewichts bewegt sich das Ergebnis an der Grenze zur Signifikanz (z-Test: p = 0,053, χ2-Test: p = 0,031, adj. OR (CI95): 0,09 (0,01 – 1,04)). Das 95 %-Konfidenzintervall (CI95) basiert auf der Normalverteilung und ist daher in Verbindung mit dem z-Test zu sehen. Ein um 1 kg höheres Gewicht könnte demnach unter Umständen die Chance, innerhalb 30 Tage nach der OP zu versterben, recht deutlich reduzieren. Wir gehen jedoch nicht davon aus, dass hier ein direkter Kausalzusammenhang zwischen dem Gewicht und der 30-Tage-Mortalität vorliegt, sondern dass es einen oder mehrere Risikofaktoren für die Schwere der Erkrankung und dem damit verbundenen Mortalitätsrisiko gibt, die auch zu einem geringeren Gewicht führen.

Die logistische Regression spielt in der Medizin und Epidemiologie eine wichtige Rolle. Es lassen sich analog zum linearen Modell ANOVA- und ANCOVA-Modelle definieren, die jedoch auf der Devianz anstelle der Varianz basieren. Man spricht deshalb auch von Devianz-Analyse. Zur Untersuchung der Modellanpassung können verschiedene Pseudo-R²-Maße verwendet werden, wobei auch AIC und BIC für Modellvergleiche zur Verfügung stehen. Häufig wird die logistische Regression auch für die binäre Klassifikation eingesetzt. In jedem Fall sollte ein gefittetes Modell immer einer gründlichen Modelldiagnostik unterzogen werden. Das Simpson-Paradoxon oder Multikollinearität können auch im Zusammenhang mit der logistischen Regression auftreten. Soll mit Hilfe einer statistischen Modellwahl ein möglichst gutes logistisches Regressionsmodell gefunden werden, so sollte dies mit großer Sorgfalt und unter Verwendung einer internen oder externen Validierung erfolgen, um ein Bias zu vermeiden. Generell empfehlen wir bei komplexen Regressionsanalysen immer einen Statistiker zu konsultieren.